重點
不熟悉快速排序法的讀者,可以閱讀最下方的兩段落來溫習一下 快速排序的基本步驟, 時間複雜度 & 空間複雜度
本文是針對快速排序法中最重要的一個環節 樞軸選擇 進行探討
樞軸選擇:樞軸的選擇對快速排序的性能有著顯著影響。常見的優化策略包括隨機選擇樞軸、三數取中法(Median-of-three)和Tukey’s Ninther,這些方法旨在減少最壞情況發生的概率,提高演算法在各種數據分布下的性能。樞軸選擇的好可以避免複雜度達到(O(n^2))
實驗結果
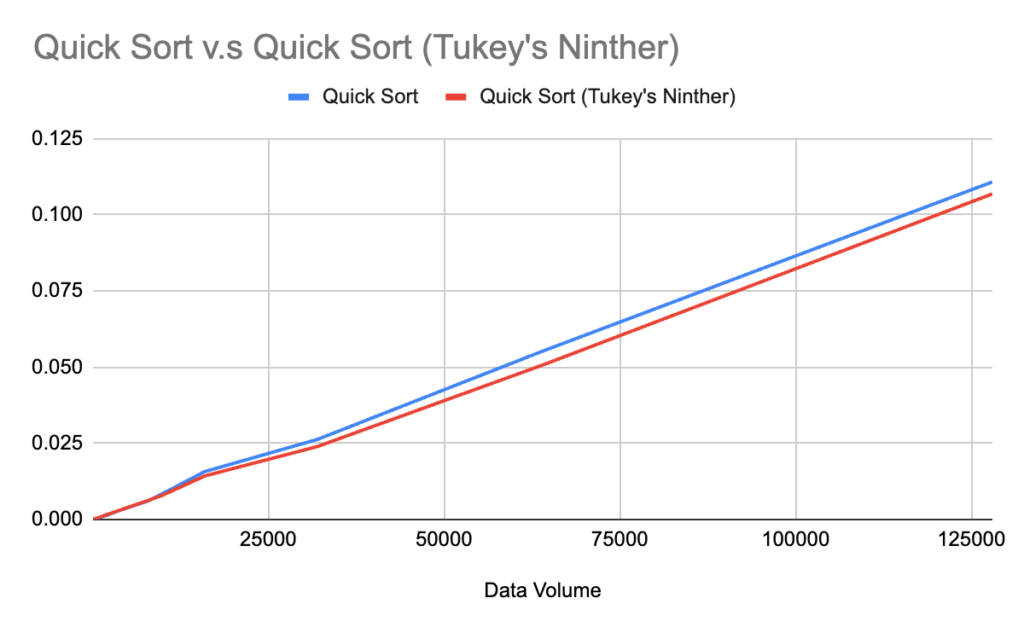
從下圖中可以得知,當數據量超過10000筆之後,大部分的情況下Tukey’s Ninther的運行速度都比Quick sort還快.其原理並不難理解,有別於傳統的快速排序法,Tukey’s Ninther一開始就先透過抽樣的方式,把中位數設定為Pivot,讓分區變得更為平均.
建議想了解概念的讀者看一下這部影片三數取中法(Median-of-three),三數取中法跟Tukey’s Ninther方法概念很接近,但更好理解.
有時間的讀者也可以用我的Performance Test 程式碼進行實際的測試
基本步驟
- 選擇樞軸(Pivot):從陣列中選擇一個元素作為樞軸,排序過程將圍繞這個樞軸進行。
- 分區(Partitioning):重新排列陣列,使得所有比樞軸小的元素都排在樞軸的前面,而所有比樞軸大的元素都排在樞軸的後面。在這個分區結束之後,樞軸處於其最終位置。
- 遞迴排序:遞迴地將小於樞軸的部分和大於樞軸的部分分別進行快速排序。
時間複雜度 & 空間複雜度
- 時間複雜度:
- 最好情況:(O(n\log n)),當每次分區都能將陣列分為兩個大致相等的部分時。
- 平均情況:(O(n\log n)),對於隨機分布的數據,快速排序的平均性能非常接近其最佳性能。
- 最壞情況:(O(n^2)),當每次分區操作都將陣列分為兩部分,其中一部分包含所有元素,另一部分為空,例如,當陣列已經是排序好的或者所有元素相同。
- 空間複雜度:快速排序的空間複雜度為(O(\log n)),這是因為快速排序是遞迴進行的,需要棧空間存儲遞迴調用的信息。在最壞情況下,如果遞迴樹變成線性的,空間複雜度可以達到(O(n))。
